This is a follow-up article on my play through of Exapunks, feel free to read the prologue to this series to learn about the background. In this article, we will briefly talk about implementing a recursion in a low-level setting.
As we know, we can do a simple recursion easily with languages like Python, as follows
def fibonacci(count: int, current: tuple[int, ...] | None = None) -> tuple[int, ...]:
if current and len(current) == count:
return current
elif count <= 2:
return (1, 1)[:count]
else:
return fibonacci(
count,
(current + (current[-2] + current[-1],)) if current else fibonacci(2),
)
As you can see, we repeatedly call the same function, with slightly different arguments each time. The result is constructed incrementally, and eventually we return it to the caller.
The same thing can be represented in a more functional manner, as follows:
def fibonacci(count: int) -> tuple[int, ...]:
return reduce(
lambda current, incoming: (current + (1,))
if incoming < 2
else (current + (current[-2] + current[-1],)),
range(count),
tuple(),
)
Like the previous example, we also accumulate the result incrementally. However, we don’t call the function again and again this time.
For the record, if this is done as a loop:
def fib3(count: int) -> tuple[int, ...]:
result = tuple()
for incoming in range(count):
result = result + ((1,) if incoming < 2 else (result[-2] + result[-1],))
return result
Very similar to the functional approach, and the result is also constructed incrementally. We are not comparing how each of these works, or how they are better than the rest, this time we are looking into implementing recursion in a low level setting, as it is not as straight-forward.
For instance, in Unknown Network 1, you are tasked to traverse the network, and grab a file back to your host.
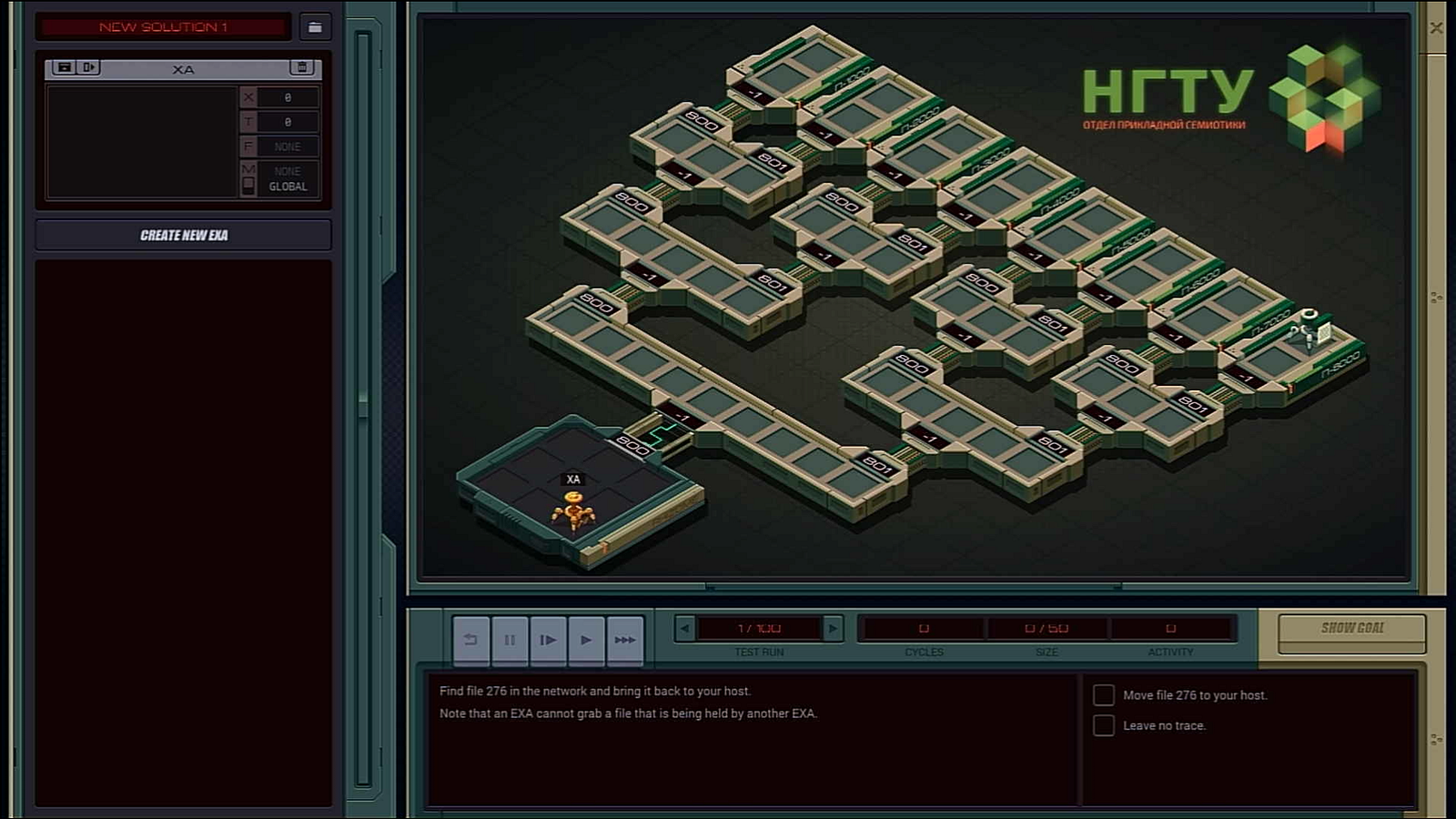
The file is always located in the 4th level, and the network always forms a binary tree. There are multiple ways to traverse the network, and for this I am choosing the most obvious way — breadth first search.
I would start by traversing the left-hand side of the tree.
LINK 800
COPY 3 T
MARK LFORK
FJMP SNATCH
SUBI T 1 T
LINK 800 ; go to the left
JUMP LFORK
MARK SNATCHSo what the code does is to rely on a counter stored in the T register to decide if it should go deeper. Every step it is jumping (through LINK command) it is decremented by 1. When it is done reaching the end of the tree, we move on to the next task.
If you have been programming long enough, you will eventually see experienced engineers shouting “GOTO considered harmful”. However, it is usually the only way we repeat certain actions, especially when we don’t know for how many times we should do that.
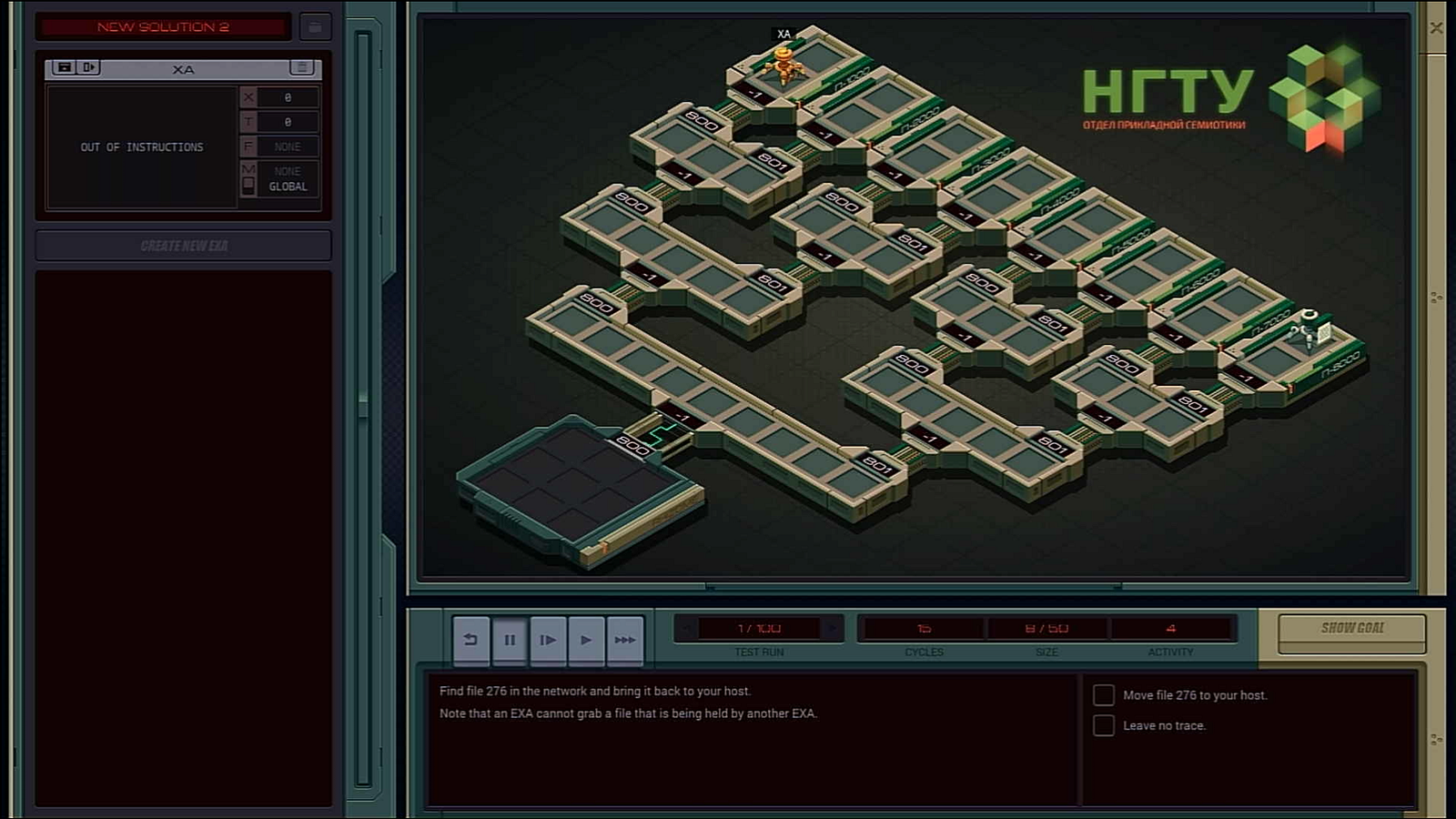
So, how do we traverse the right-hand side?
LINK 800
COPY 3 T
MARK LFORK
FJMP SNATCH
SUBI T 1 T
REPL RFORK ; spawn a new exa here
LINK 800
JUMP LFORK
MARK RFORK
LINK 801 ; go to the right
JUMP LFORK ; go back to the main loop
MARK SNATCHJust spawn a new EXA, right before we jump to another host on the left. Then because it is placed in a loop, the same operation repeats itself on every level.
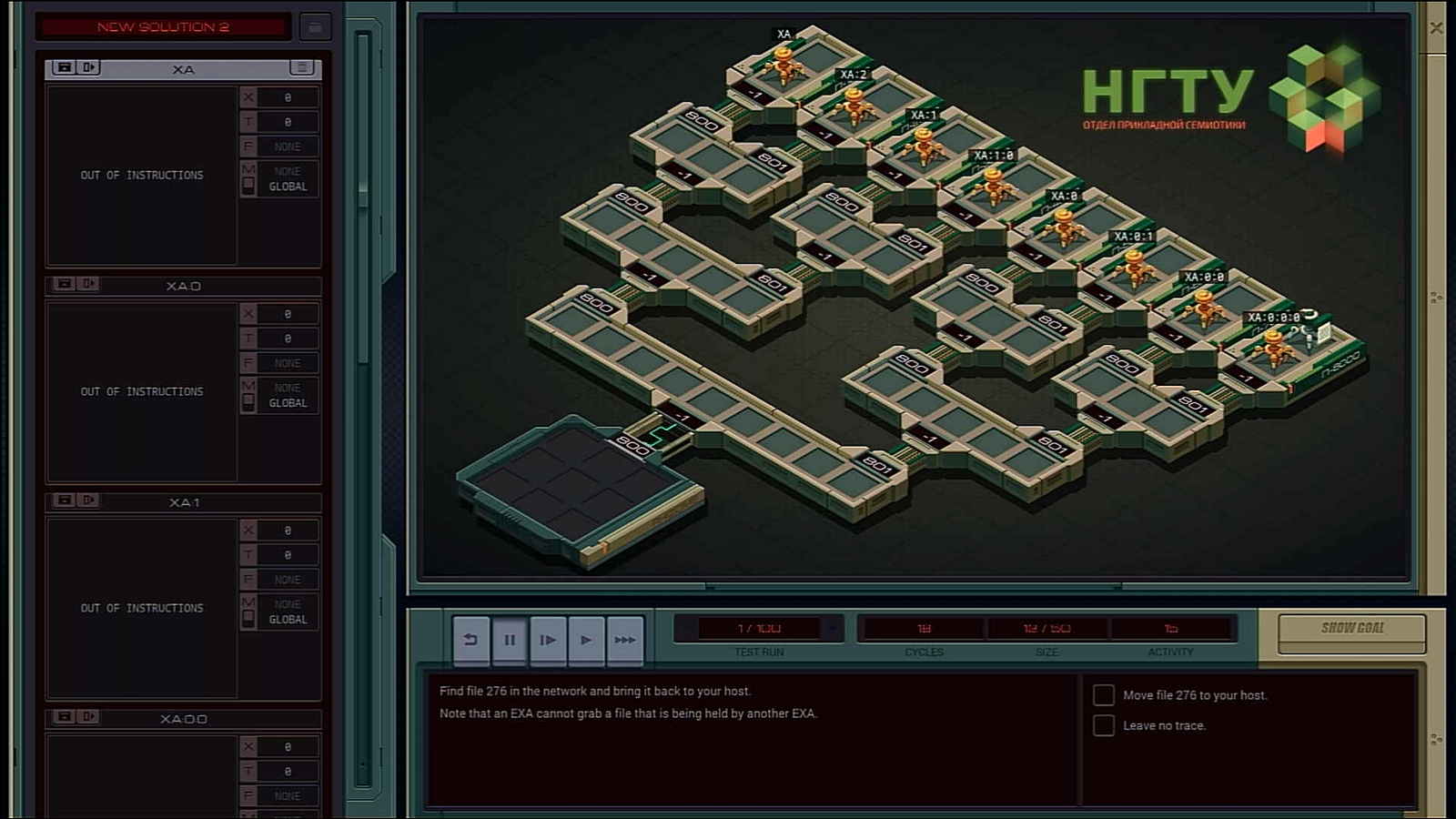
When we achieve this, then the rest is trivial, we can start filling in the implementation detail of SNATCH.
MARK SNATCH
KILL
GRAB 276
LINK -1
LINK -1
LINK -1
LINK -1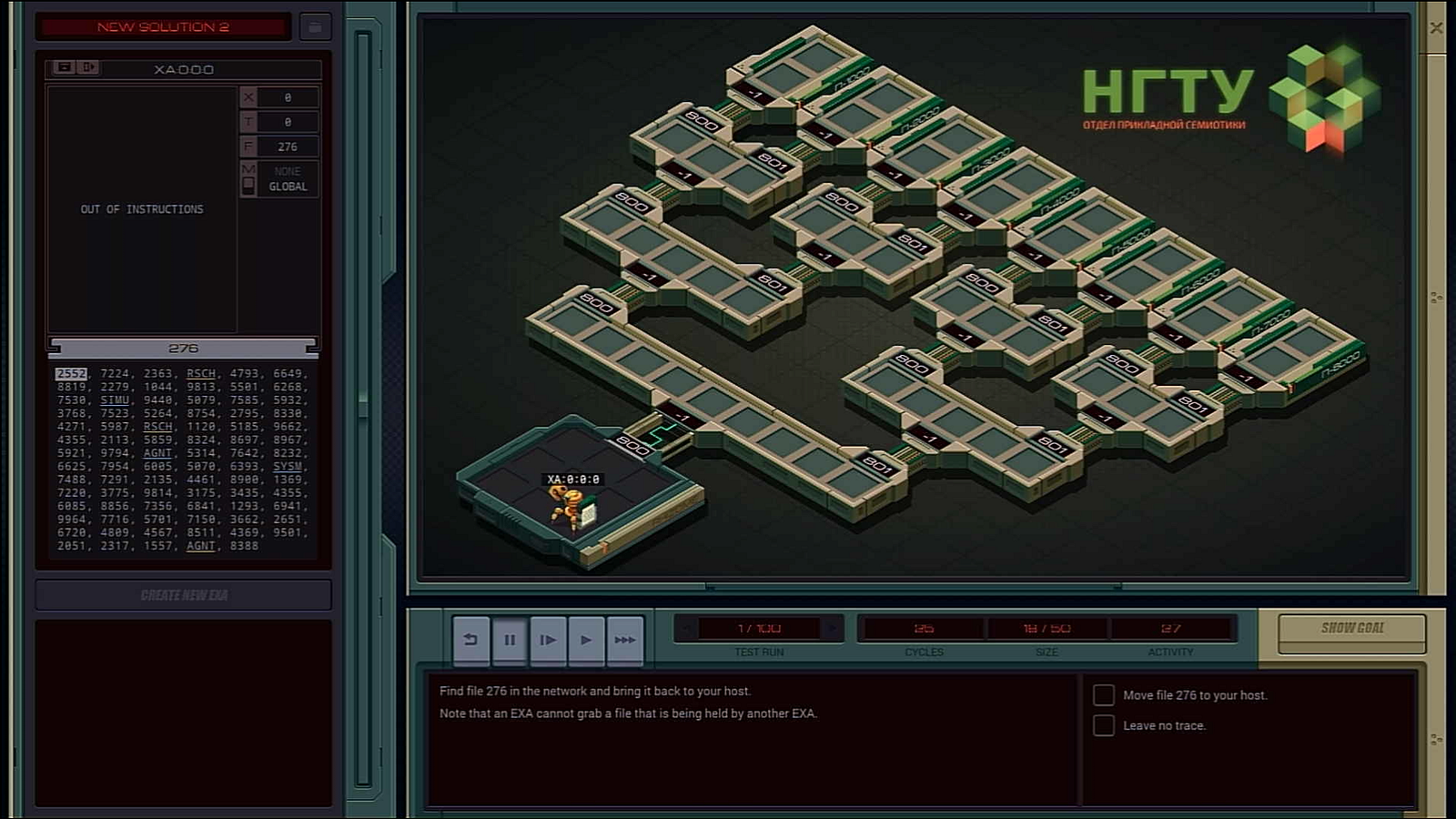
There you have it, this is how we implemented breadth first search through recursion in a low-level setting.
Leave a Reply